Як виглядає парабола?
Пара́бола (від грец. παραβολή) — геометричне місце точок, що рівновіддалені від точки і прямої. Одна з кривих другого порядку. Точка зветься фокусом, а пряма — директрисою.
Як знайти точку параболи?
Для того, щоб знайти точки перетину параболи функції у = ах2 + bx + c з віссю абсцис, необхідно скласти рівняння ах2 + bx + c = 0 і знайти його корені. Слід зазначити, що значення х, при яких функція у = ах2 + bx + c дорівнює нулю, називають нулями квадратичної функції!
Як знайти область визначення параболи?
Область значень: Щоб знайти область значень, потрібно:визначити напрям віток параболи і знайти ординату вершини параболи 𝒚𝟎. 𝒚∈[𝒚в;+∞) 𝒚=𝒂𝒙𝟐+𝒃𝒙+𝒄𝒂<𝟎 1. Область визначення: 𝒙∈−∞;+∞.
Коли парабола вниз?
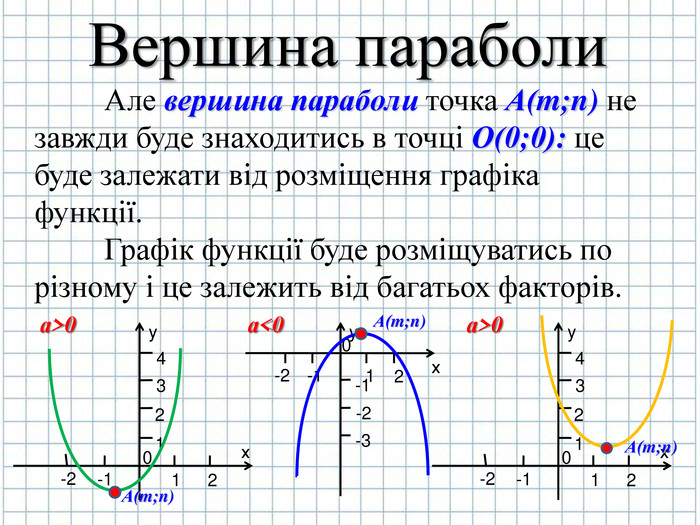
Якщоa>0, парабола відкривається вгору. Якщоa<0, парабола відкривається вниз.
Таким чином, парабола – це сукупність точок, (x,y) рівновіддалених від лінії y=−b і точки фокусування (0,b). Відстань до лінії – це вертикальни …
У відео про те як побудувати різні типи парабол, від чого залежить напрям віток та як знайти координати вершини параболи.
Графіком функції y = k x 2 , k ≠ 0 є парабола з вершиною на початку координат і з вітками, напрямленими вгору, якщо k > 0 та вниз, якщо k < 0.